Blog

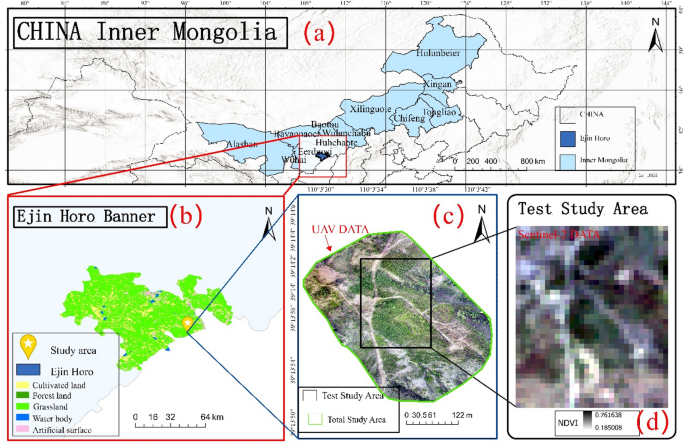
Study area and data source

The study area is the Erlintu mining area in Inner Mongolia, China. Mining activities have significantly disturbed the local ecological environment, particularly affecting vegetation, soil, and water resources. Located in the eastern part of the Ordos Plateau, the area is characterized by plateau erosion hills and has a temperate climate with average annual temperatures ranging from 6.2 °C to 8.7 °C and annual precipitation between 379 and 420 millimeters. Due to these specific climate and terrain conditions, the region has sparse vegetation, significant gully formation, and perennial surface runoff, resulting in ecological vulnerability³¹. A schematic of the location of the study area, UAV imagery, and Sentinel II imagery are shown in Fig. 1(a)\(b) below. Use the ArcGIS Pro software of Esri Company (version 3.4.0; Esri, 2024) conducts geographic data processing and mapping, including boundary extraction, coordinate system transformation, and thematic map rendering³².

Map of study area. (a,b) Show the location of the study area, (c) shows the UAV image of the study area, and (d) shows the Sentinel-2 satellite image of the test study area.

The satellite data is derived from the L2A level imagery of the Sentinel-2 satellite, specifically the image acquired on September 5, 2023, with 1% cloud cover. This image was processed using the European Space Agency’s (ESA) Sen2Cor algorithm for atmospheric correction and was obtained through the AIearth platform³³. As in Fig. 1 (d).

The UAV data was collected at the same time as the satellite data, using the DJI M210 RTK UAV platform equipped with an X5S multispectral camera (15 mm focal length). The flight parameters were set to an altitude of 80 m, with 70% forward overlap and 70% side overlap, ensuring a ground sampling distance (GSD) of 1.8 centimeters. To reduce the impact of lighting variations on data quality, the flight speed was controlled below 6 m per second to prevent motion blur. For data processing, Pix4Dmapper 4.5.6 software was utilized, involving steps such as feature extraction and matching, aerial triangulation, bundle adjustment, orthorectification, and mosaicking, ultimately yielding accurate multispectral band data³⁴. As in Fig. 1 (d). The results are shown in Fig. 1(c).

Research method

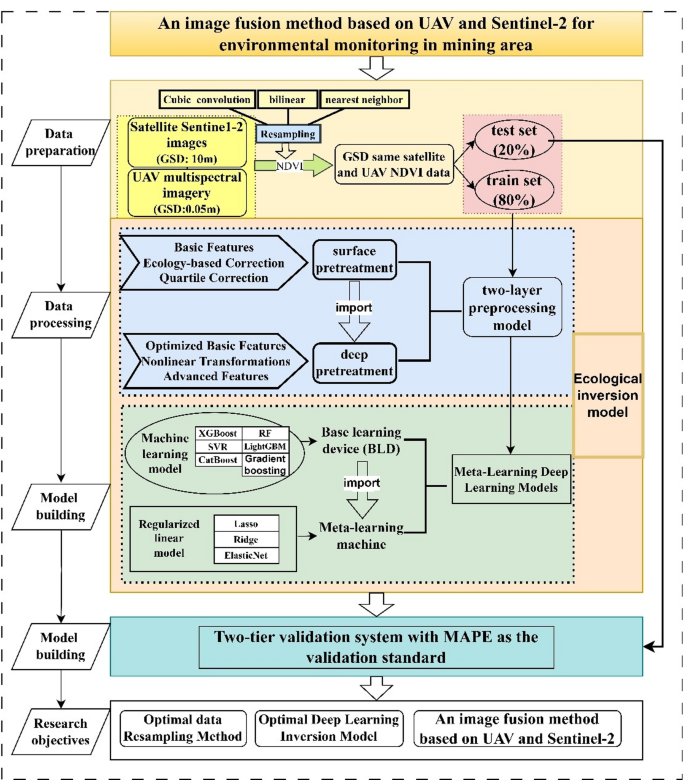
This study proposes a novel method for fusing UAV and Sentinel-2 imagery, specifically designed to address the challenges of spatial-temporal resolution mismatch and to enhance the accuracy of environmental monitoring in small-scale, heterogeneous mining environments. The technical roadmap, which integrates data preprocessing, advanced feature engineering, and an ensemble learning-based inversion model, is illustrated in Fig. 2. The key steps are as follows: (1) First, acquire multispectral UAV images (native Ground Sampling Distance (GSD) of 0.05 m) and Sentinel-2 L2A satellite images (10 m GSD for relevant bands) of the Erlintu mining area, both captured on September 5, 2023. Perform essential initial image preprocessing, including radiometric calibration for the UAV imagery and ensuring atmospheric correction (inherent in Sentinel-2 L2A products).Perform spatial registration through visual interpretation and geometric correction to ensure excellent spatial correlation between multi-source datasets at sub-pixel accuracy levels. (2) To establish a common analytical scale, resample both the UAV NDVI data and the Sentinel-2 NDVI data (using resampling techniques detailed in Sect. 2.2.1).This results in UAV NDVI and Sentinel-2 NDVI datasets both at a 0.1 m spatial resolution. The resampled UAV NDVI data serves as the high-resolution reference. The combined dataset, using pixel pairs from the aligned 0.1 m resolution NDVI maps, is then split in a 4:1 ratio to construct training and testing sets for the inversion model. (3) Construct a two-layer preprocessing model (detailed in Sect. 2.2.2). Given the inherent differences in sensor characteristics and the information alteration potentially introduced by resampling both UAV (down-sampling) and Sentinel-2 (up-sampling) data, this model aims to normalize data distributions, enhance relevant features, and extract multi-dimensional information. The first layer is the basic processing layer for fundamental statistical feature calculation and data correction. The second layer is the advanced processing layer to further extract multi-dimensional and non-linear features, laying a robust foundation for the subsequent learning process. (4) Build a stacked ensemble learning inversion model (detailed in Sect. 2.2.3). The base learner layer employs six diverse machine learning regression models: Random Forest (RF), XGBoost (XGB), Support Vector Regression (SVR), Gradient Boosting (GB), LightGBM, and CatBoost, chosen for their varied strengths in handling complex data. The meta-learner layer utilizes LightGBM, selected after comparative analysis to optimally weight and combine the predictions from the base learners. (5) Input all resulting NDVI predictions into the validation system (detailed in Sect. 2.2.4). Through comparative analysis of different resampling methods and model configurations, select the optimal data resampling strategy and inversion model. This process aims to deliver a multi-source image fusion method suitable for achieving small-scale, long-term, high-precision ecological monitoring of mining area surfaces^35,36.

In the formula, ρ is the band reflectance, RED is the red band, and NIR is the near-infrared band.

A schematic diagram illustrating the technical route of the thesis.

Resampling methods

To address the significant discrepancy in original spatial resolutions between Sentinel-2 (e.g., 10 m GSD for red and NIR bands) and UAV (0.05 m GSD) NDVI data, and to establish a common analytical resolution of 0.1 m, we employed distinct resampling strategies for each data source. The Sentinel-2 NDVI data was up-sampled from its native resolution to the target 0.1 m resolution. Concurrently, the UAV NDVI data was down-sampled (or aggregated) from its original 0.05 m resolution to 0.1 m, serving as the high-resolution reference for model training and accuracy validation after resampling. This consistent 0.1 m resolution ensures spatial conformity for pixel-level fusion and comparison³⁷It is important to acknowledge that aggressive up-sampling of Sentinel-2 data (e.g., from 10 m to 0.1 m, a 100-fold increase in pixel density per axis) can lead to smoothing of fine details or the potential introduction of interpolation artifacts, as it does not generate new genuine information present at the finer scale. Similarly, down-sampling the UAV data, while necessary for matching resolutions, involves an aggregation or selection process that can also alter the original very-high-resolution information. The choice and impact of specific resampling methods are therefore critical and evaluated in this study.To comprehensively assess the impact of different up-sampling methods for Sentinel-2 NDVI data on inversion accuracy, this study utilized three common spatial resampling techniques: nearest neighbor, bilinear interpolation, and cubic convolution. The principles and calculation formulas for each method are as follows³⁸:

Nearest neighbor

The nearest neighbor resampling method assigns the value of the closest source pixel to the target pixel. This method is simple and efficient, effectively preserving the original data’s spectral features. However, it can cause spatial discontinuities in the image, especially at edges, leading to noticeable aliasing effects. Its calculation formula is:

Pout (x, y) is the pixel value of the output image at position (x, y), Pin is the input image, and round(x) and round(y) are the nearest integers to x and y, representing the closest source pixel position.

Bilinear interpolation

Bilinear interpolation improves the visual effect and spatial continuity of the image by performing a linear weighted calculation on the pixel values of the adjacent 2 × 2 window in the source image. However, it may cause some image blurring and mixing of spectral features. Its calculation formula is:

Cubic convolution

The Cubic Convolution method performs cubic polynomial interpolation based on a 4 × 4 neighborhood window, effectively balancing the preservation of spatial details and edge smoothness in the image, and excelling in both geometric accuracy and visual quality. However, due to the complexity of the computation, the processing time is significantly increased. The formula for this method is:

Here, k(t) k(t) k(t) is the cubic interpolation kernel, typically chosen as:

In the formula, t is the relative position to the target pixel, and (x_i, y_i) are the coordinates of the 16 source pixels surrounding the target pixel.

Construction of the two-layer preprocessing model

Given the inherent differences in sensor characteristics (e.g., spectral response functions, signal-to-noise ratio) and the information alteration potentially introduced by resampling both UAV (down-sampling from 0.05 m to 0.1 m) and Sentinel-2 (up-sampling from ~ 10 m to 0.1 m) data, a robust two-layer preprocessing model was designed. This model aims to normalize the data distributions between the two sources, enhance features relevant for predicting UAV-equivalent NDVI from Sentinel-2 data, and extract multi-dimensional information to facilitate a more effective learning process for the subsequent inversion model. The two-layer preprocessing combines data optimization and feature extraction methods to improve data quality and enhance model performance. The first layer of the two-layer preprocessing is the basic processing layer, which mainly includes three parts: preliminary statistical analysis, quantile correction, and ecological zoning correction. The preliminary statistical analysis primarily involves calculating basic statistical features of the UAV and satellite data, such as minimum, maximum, mean, median, and standard deviation. The purpose of this process is to comprehensively assess the distribution characteristics of the data, provide necessary information for subsequent models to identify potential anomalies and biases in the dataset, and lay the foundation for the following correction steps. Next, quantile correction³⁹ is performed as a key technique to reduce systematic biases between sensors. It precisely adjusts the key quantiles of the satellite data (such as 10%, 25%, 50%, 75%, and 90%) to match the corresponding quantiles of the UAV data. Finally, the study also implemented ecological zoning correction⁴⁰. Considering that NDVI values in different ecological zones may be influenced by various environmental factors, we divided the data into different ecological zones based on the range of NDVI values and applied specific multiplier adjustments to each zone. For example, water bodies and built-up areas typically have lower NDVI values because their reflective properties differ significantly from those of vegetation. Therefore, we made appropriate adjustments to the data in these zones to more accurately reflect their actual characteristics.

The second layer of the two-layer preprocessing is the advanced processing layer, which takes the data processed by the basic layer as input and further extracts multidimensional features from it. First, basic statistical features such as mean, median, maximum, minimum, standard deviation, as well as skewness and kurtosis, are extracted again from the data processed by the basic layer, providing the subsequent models with basic descriptive information about the data to help them understand its central tendency and distribution shape. At the same time, to capture complex relationships and potential patterns in the data, advanced statistical features, including autocorrelation and partial autocorrelation coefficients, are also introduced. Additionally, considering the nonlinear characteristics of NDVI data, various nonlinear transformations⁴¹, such as logarithmic, square root, and reciprocal transformations, are applied to the data to linearize the nonlinear relationships, thereby helping the model handle extreme values and non-standard distributions more effectively.

\(\:{x}_{i}\)represents the value of the i-th cell in the grid, and n n n is the total number of cells in the grid.

Construction of an inversion model based on an ensemble learning architecture

This study constructs an ensemble learning framework based on the stacking architecture⁴².The primary motivation for employing Stacking is to overcome the limitations of individual machine learning models in accurately predicting high-resolution (0.1 m) UAV-equivalent NDVI from preprocessed 0.1 m Sentinel-2 NDVI data and its derived features.Single models often struggle to capture the diverse features and nonlinear relationships in the data. Therefore, by integrating the strengths of multiple models, we can complement each other’s limitations, thereby improving prediction accuracy and generalization ability.

The model architecture consists of two layers: the first layer is the base learner layer, and the second layer is the meta-learner layer.

Base learner layer

This layer consists of six distinct regression models, selected for their proven efficacy in handling complex, non-linear relationships often encountered in remote sensing data, and their diverse algorithmic approaches which allow them to capture different facets of the NDVI data. The rationale behind selecting these specific base learners is to foster model diversity, a key factor for successful Stacking. This diversity is achieved by including tree-based ensemble methods (Random Forest, XGBoost, Gradient Boosting, LightGBM, CatBoost) known for their robustness and ability to model feature interactions, and a kernel-based method (Support Vector Regression) effective in high-dimensional spaces. The pre-determined hyperparameters for each base learner, which were established based on a combination of common best practices in remote sensing literature, preliminary exploratory experiments on a subset of the data, and refined through an optimal parameter search (as detailed in the Hyperparameter Tuning section below), are as follows.

Random Forest Regression (RF): Configured with 1000 decision trees (n_estimators). To control model complexity and prevent overfitting, the maximum depth of each tree (max_depth) was set to 10, the minimum number of samples required to split an internal node (min_samples_split) was 10, and the minimum number of samples required at a leaf node (min_samples_leaf) was 4. The number of features considered for the best split at each node (max_features) was set to the square root of the total number of input features. A random_state of 42 was used for reproducibility.XGBoost(XGB): Implemented with 1000 boosting rounds (n_estimators) and a conservative learning rate (learning_rate) of 0.01 to ensure stable convergence. The maximum tree depth (max_depth) was 3. The subsample ratio of the training instance for each tree (subsample) was 1.0 (using all samples for each tree, but randomness is introduced by feature subsampling), while the subsample ratio of columns when constructing each tree (colsample_bytree) was 0.9. The minimum sum of instance weight (hessian) needed in a child (min_child_weight) was 5. A random_state of 42 was used.Support Vector Regression (SVR): Utilized a Radial Basis Function (RBF) kernel (implied by gamma parameter, please confirm if RBF was used, if not, specify the kernel type). The regularization parameter C was set to 10, controlling the trade-off between achieving a low training error and a low testing error (generalization). The kernel coefficient gamma was set to ‘auto’ (typically 1/n_features for RBF), and the epsilon (epsilon) in the epsilon-insensitive loss function was 0.2, defining the margin within which no penalty is associated in the training loss function.Gradient Boosting (GB): Configured with 1000 boosting stages (n_estimators) and a learning rate (learning_rate) of 0.01. The maximum depth of individual regression estimators (max_depth) was 5. The minimum number of samples required to split an internal node (min_samples_split) was 5, and the minimum number of samples required at a leaf node (min_samples_leaf) was 2. The fraction of samples used for fitting the individual base learners (subsample) was 0.8, introducing stochasticity. A random_state of 42 was used.LightGBM LightGBM Regression: Set with 1000 boosting iterations (n_estimators) and a learning rate (learning_rate) of 0.01. The maximum tree depth (max_depth) was 5, and the maximum number of leaves per tree (num_leaves) was 31. The minimum number of data points in a leaf (min_child_samples or min_data_in_leaf) was 20. Both subsample (bagging_fraction) and feature_fraction (colsample_bytree) were set to 0.8. A random_state of 42 was used.

CatBoost Employed 1000 iterations (iterations) with a learning rate (learning_rate) of 0.01. The maximum tree depth (depth) was 6. The L2 regularization coefficient (l2_leaf_reg) was 3. A random_state of 42 was used, and training verbosity was turned off.

All model parameters were determined through optimal parameter search methods to ensure the best performance of each model on the dataset.

Meta-learner layer

The outputs from each base learner in the first layer, generated via a k-fold cross-validation scheme to prevent information leakage, serve as input features for the second-layer meta-learner. The primary function of the meta-learner is to optimally integrate these diverse base-level predictions, thereby enhancing overall prediction accuracy and generalization. Initially, we investigated several candidate models for the meta-learner role, including regularized linear regression models such as Lasso regression, Ridge regression, and ElasticNet regression. Lasso regression, with its L1 regularization, can perform implicit feature selection by shrinking the coefficients of less important base learners toward zero, potentially improving model interpretability and reducing variance. Ridge regression, utilizing L2 regularization, effectively handles multicollinearity among base learner predictions and prevents overfitting by penalizing large coefficients. ElasticNet regression combines L1 and L2 penalties, leveraging the advantages of both approaches. For these linear meta-learners, hyperparameters were tuned using a nested cross-validation approach based on the first-level predictions (meta-features).

However, after empirical evaluation and comparison, a LightGBM (Light Gradient Boosting Machine) model was ultimately selected as the final meta-learner. LightGBM, a gradient boosting framework employing tree-based learning algorithms, was chosen due to its efficiency, ability to capture complex non-linear relationships between base learner outputs, and strong performance observed in preliminary experiments for this meta-learning task. Key hyperparameters for the LightGBM meta-learner, such as n_estimators, learning_rate, max_depth, num_leaves, and reg_alpha/reg_lambda, were carefully optimized using a randomized search with 5-fold cross-validation on the meta-feature training set, targeting MAPE minimization. For instance, a typical search space for LightGBM included n_estimators, learning_rate in [0.01, 0.05, 0.1], and max_depth. The best-performing hyperparameter set was subsequently utilized for the final meta-learner.

The rationale for adopting a Stacking architecture with such a meta-learner lies in fully leveraging the diverse predictive capabilities of each base learner. While individual models may excel at capturing specific patterns or performing well under certain data conditions, the meta-learner learns to intelligently weight or combine their outputs, compensating for individual model weaknesses and mitigating the risk of overfitting to the idiosyncrasies of any single base model. This synergy among multiple models typically results in a more stable, robust, and accurate overall prediction, capable of capturing both linear and complex non-linear features present in the relationship between the input satellite data (and its engineered features) and the target UAV NDVI.

To ensure robust model development and prevent overfitting during both base learner training (for generating meta-features) and meta-learner training, a consistent 5-fold cross-validation (CV) strategy was employed throughout the Stacking framework. First-level predictions (meta-features) for the training data were generated by training base learners on 4 folds and predicting on the remaining 1 fold, iterating this process 5 times so that each data point in the training set has an out-of-fold prediction. For the test set, each base learner was trained on the entire training set before making predictions. The meta-learner was then trained on these out-of-fold predictions from the training set and evaluated on the predictions made on the test set. This rigorous validation strategy enhances the stability and reliability of the final inversion model, providing a more trustworthy estimate of its performance on unseen data.

The performance of the final Stacking model, as well as the intermediate base learners and alternative meta-learners, was assessed using a comprehensive suite of metrics, including Mean Absolute Percentage Error (MAPE) as defined in Sect. 2.2.4. These metrics provide a thorough evaluation of the model’s accuracy, bias, and goodness of fit.

Accuracy verification method

In this study, the NDVI values from high-resolution UAV images are used as the reference values, while the NDVI values from the original, resampled, and inverted Sentinel-2 images are used as the experimental values. 3000 paired sample points are randomly selected, and the Mean Absolute Percentage Error (MAPE) is calculated to reflect the degree of deviation between the experimental values and the reference values⁴³. The standard calculation method for MAPE is shown in Eq. (10), A larger MAPE value indicates a more severe deviation between the experimental values and the reference values, suggesting poorer performance of the resampling and inversion models, while a smaller MAPE value indicates better performance. In this study, to avoid the division by zero problems (since NDVI values can be 0), Eq. (10) was modified to Eq. (11):

Where n is the number of observations, \(\:{y}_{i}\) is the i-th UAV NDVI value, and \({\hat{y}}_{i}\) is the i-th satellite NDVI predicted value.

Furthermore, taking into account the high-resolution characteristics of the interpolated satellite data, a centered moving average with a window of 3-time steps is applied to smooth the data. Forward fill and backward fill are used to handle missing values at the boundaries. Subsequently, the relative error is calculated based on the smoothed data, as shown in Eq. (12):

where \(\:\overline{{y}_{i}}\) and \(\:\widehat{\overline{{y}_{i}}}\) are the values after window averaging.

For y1, y2, y3, …, the calculation formula for the moving average \(\:\overline{{y}_{i}}\) with a window size of k (where k = 3 in this study) is:

This dual-layer validation system not only considers the continuity characteristics of the data, but also adapts to the scale changes of NDVI values under different vegetation cover conditions, providing a reliable evaluation basis for the quantitative assessment and subsequent optimization of model performance.